[빅데이터분석기사 필기 요약] [빅분기 4과목 요약] IV. 빅데이터 결과 해석 - 요약 (1)

[빅데이터분석기사 필기 4과목] IV. 빅데이터 결과 해석
 
01. 분석 모형 평가 및 개선
 
 

• 분석모형 평가기준: 일반화 가능성/ 효율성/ 예측과 분류의 정확성

 

일반화 가능성	효율성	예측과 분류의 정확성
데이터를 확장하여 적용할 수 있는가 (안정적인 결과를 제공하는가)	적은 입력변수가 필요할수록 효율성이 높은 것으로 평가함	정확성 측면에서 평가함

 
 

• 모형 평가지표

 

회귀 모형 (예측 모형) 평가지표	분류 모형 평가지표
- 실제값/ 예측값/ 평균값 - 오차제곱합 SSE - 전체제곱합 SST - 회귀제곱합 SSR - 결정계수 R² = SSR / SST (and 수정된 결정계수) - Mallow's Cp	- 혼동 행렬 Confusion Matrix - 정확도/ 민감도/ 정밀도/ F1-score - ROC Curve - AUC (Area Under ROC) - 이익 도표 Gain Chart

 
 

• 회귀 모형 평가지표: 제곱합(SSE/ SST/ SSR)/ 결정계수/ 수정된 결정계수/ Mallow's Cp

 

제곱합 Sum of Square	결정계수 R²	수정된 결정계수 R²adj	Mallow's Cp
SST = SSE + SSR - SST: 실젯값-평균값의 차이 - SSE: 실젯값-예측값의 차이 - SSR: 예측값-평균값의 차이	R² = SSR / SST (0~1) - 회귀모형이 실젯값을 얼마나   잘 나타내는지에 대한 비율 - 선형회귀의 성능 검증지표 - 독립변수 개수가 많은 경우,   유의하지 않아도 증가함	R²adj < R² - 결정계수의 단점을 보완함 - 적절하지 않은 독립변수를   추가할수록, 패널티를 부과함 - 수정된 결정계수는 원래   결정계수보다 항상 작다!	- 적절치 않은 독립변수 추가에   대한 패널티를 부과한 통계량 - Cp값이 작을수록, 모형은   실젯값을 잘 설명함 - p = 선택된 독립변수의 개수

 
 

• 분류 모형 평가지표: 혼동 행렬/ ROC곡선/ AUC/ 이익 도표

 

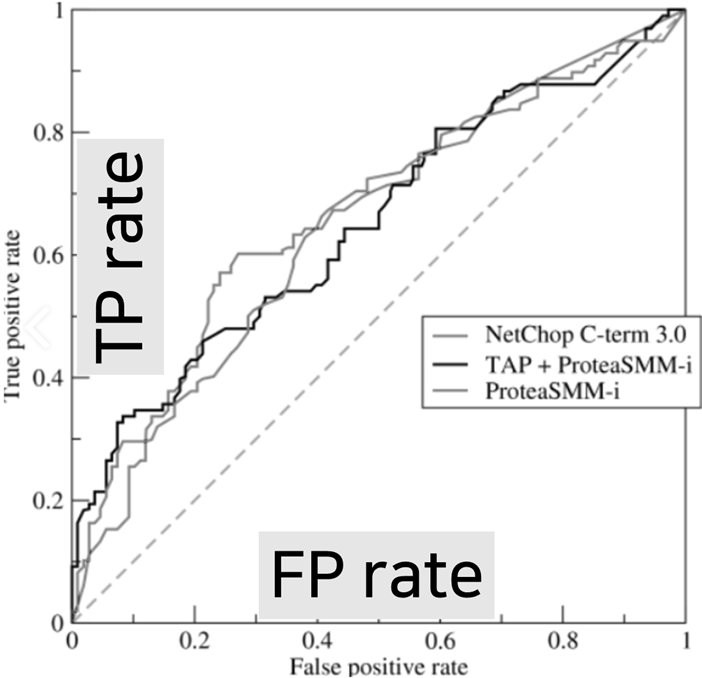
혼동 행렬	ROC Curve & AUC	이익 도표
예측값과 실제값의  일치빈도를 통해 모델 정확도 평가	X axis = FP rate Y axis = TP rate 반비례 관계 (Trade-off)	- 이익: 목표범주에 속한 개체들이   임의로 나눈 등급별로   얼마나 분포하고 있는지 나타내는 값
- TP = Pos를 Pos로 예측 (맞음) - FN = Pos를 Neg로 예측 (틀림..) - TN = Neg를 Neg로 예측 (맞음) - FP = Neg를 Pos로 예측 (틀림..)	- 곡선이 왼쪽꼭대기에 가까울수록   모델의 분류 성능이 우수하다 - AUC = ROC 곡선 아래 면적 (0.5~1.0) - AUC는 1에 가까울수록 정확도 높음	- 그래프를 분석하여 분류 성능 평가함 - 이익도표 = 이익곡선 = 리프트곡선을   통해 분류 모델의 성능을 평가한다

 
 

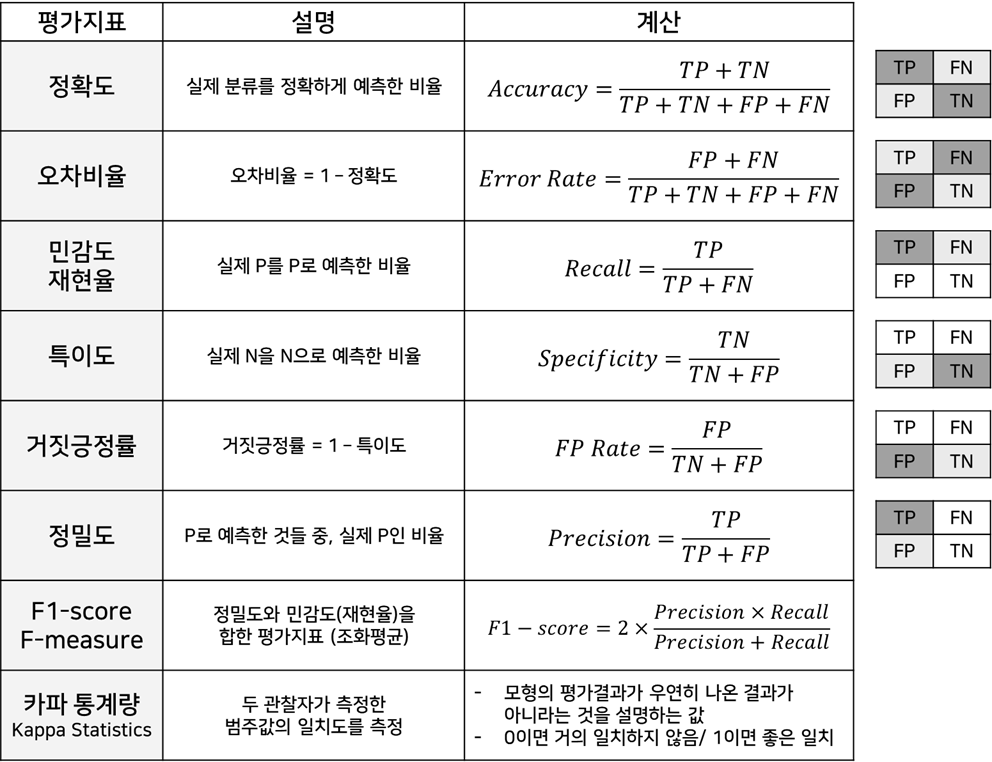
• 혼동 행렬을 이용한 분류 모형의 평가지표:

 
 

 
 
 

• 분석 모형 진단: 오류/ 검증/ 시각화/ 진단

 

분석 모형의 오류	분석 모형 검증	분석 모형 시각화	분석 모형 진단
일반화 오류 = 과대적합 - 데이터 특성 지나치게 반영 - 주변적 특성&잡음까지 묘사	홀드아웃 교차검증 - 겹치지 않도록 무작위 구분 - 학습집합: 모형 구축 - 시험집합: 성능 평가	정보 구조화 → 정보 시각화 → 정보 시각표현	분석모형의  기본가정에 대한 진단이 필요함
학습 오류 = 과소 적합 - 주어진 데이터를 덜 반영	다중 교차검증 - 같은크기 k개로 무작위 나눔  -학습집합: (k-1)개 - 시험집합: 1개	- 구조화: 수집 및 탐색/   분류/ 배열 및 재배열 - 시각화: 시각/ 분포/ 관계/   비교/ 공간 시각화	회귀모형: 잔차 산점도를 이용 - 선형성/ 독립성/ 등분산성 - 정상성(정규성)

 

---

 

• 교차검증
  - 모델의 일반화 오차에 대해, 신뢰할만한 추정치를 구하기 위한 검증기법
  - 훈련 데이터, 평가 데이터를 기반으로 하는 검증기법
• 교차검증 종류: 홀드아웃 교차검증/ 랜덤 서브샘플링/ K-Fold/ LOOCV/ LpOCV/ RLT/ 부트스트랩

 
 

 
 
 

• 홀드 아웃 교차 검증: 비복원 추출 - 랜덤하게 학습/평가데이터로 나누어 검증 (5:5, 3:7, 2:1, ...)
• 랜덤 서브샘플링: 모집단으로부터 조사대상이 되는 표본을 무작위로 추출하는 기법
• K-Fold Cross Validation:
  데이터집합을 무작위/ 동일크기/ K개의 부분집합으로 나눔 - K개의 실험결과를 종합 - 최종성능 구함

 

홀드 아웃 교차 검증	랜덤 서브샘플링	K-Fold Cross Validation
비복원 추출 랜덤하게 나눔 데이터 손실 O	랜덤 추출 홀드아웃 반복 데이터 손실 X	랜덤 추출 동등 분할 데이터 손실 X
- 계산량/비용 적음 - 평가 데이터는 학습에 사용할 수   없으므로 데이터 손실이 발생함 - 어떻게 나누느냐에 따라 결과 달라짐	- 측정/평가 비용 가장 적음↓ - 미래예측 시, 신뢰성 추정할 수 없음	- 모든 데이터를 학습/평가에 사용 가능 - K개 실험결과 종합하여 최종성능 구함 - K값 증가↑ 계산량/시간↑
- 학습 데이터: 분류기 만들 때 사용 - 검증 데이터: 매개변수 최적화 - 평가 데이터: 분류기 성능 평가	- 각 샘플들을 학습/평가에 얼마나   사용할지 횟수 제한이 없음 - 특정 데이터만 학습할 가능성 O..	- 같은 크기의 부분집합 K개 - 학습 데이터: K-1 개 - 평가 데이터: 1 개

 
 

• LOOCV (Leave-One-Out Cross Validation)/ LpOCV (Leave-p-Out Cross Validation)
• RLT (Repeated Learning-Testing)/ Bootstrap

 

LOOCV	LpOCV	RLT	Bootstrap
- K-Fold와 같은 방법(K=N) - 교차검증 N번 반복 - 가능한 많은 데이터 학습 가능	- p개 샘플을 테스트에 사용 - 교차검증 nCp번 반복 - nCp = n! / (n-p)!p!	- 비복원 추출 - 랜덤하게 나눔 - 에러/ 평균오류율 계산	- 단순랜덤 복원추출 - 복원추출이므로 중복 O - 동일크기 표본 여러개 생성
- 계산량/시간/비용 가장비쌈↑ - 작은 크기에 데이터에 적합	- 계산시간 부담 매우 큼↑	① 랜덤하게 학습/검증 분리 ② 학습데이터로 훈련 ③ 검증데이터로 오류 계산	- 특정 샘플이 학습데이터에   포함될 확률=약 63.2% - 선택되지 않을 확률=약 36.8%
- 전체 데이터: N개 - 학습 데이터: N-1 개 - 평가 데이터: 1개	- 전체 데이터: N개 - 학습 데이터: N-p 개 - 평가 데이터: p개	④ 2,3단계를 2회 더 반복 ⑤ 평균오류율 E = ∑Ei / N	- 학습데이터에 한 번도   포함되지 않은 데이터는   평가(테스트)에 사용됨

 

---

 

• 모집단/ 모수/ 표본/ 통계량

 

모집단 Population	모수 Parameter	표본 Sample	통계량 Statistics
분석/관심 대상 전체	모집단을 설명하는 어떤 값 모집단의 특성을 나타내는 값	모집단 일부 모집단 분석을 위해 추출함	표본의 특성을 나타내는 값

 
 

 
 
 

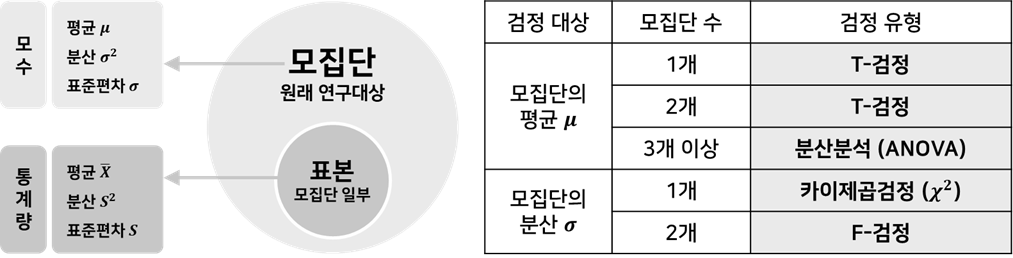
• 모집단 평균에 대한 유의성 검정: Z-검정/ T-검정/ 분산분석 ANOVA
• 모집단 분산에 대한 유의성 검정: 카이제곱검정/ F-검정

 

Z-검정	T-검정	분산분석 ANOVA	카이제곱검정	F-검정
검정통계량 분포를 귀무가설 하에서 정규분포로 근사할 수 있는 통계검정	검정통계량이 귀무가설 하에서 T-분포를 따르는 통계검정	- 2개 이상의   집단간 비교 - 일원: 독립변수 1개 - 이원: 독립변수 2개	- 관찰빈도-기대빈도가   유의하게 다른가 - 2개 집단간 동질성 - 카이제곱분포에 기초	- 두 표본의 분산이   유의하게 다른가 - F-분포에 기초
- 모분산을 알고 있음 - 추출된 표본이 같은   모집단에 속하는가	- 모분산 모르는 경우 - 두 집단간 평균 비교	- 분산비교로 얻은   F-분포를 이용함	- 모집단이 정규분포 따름 - 분산 알고 있는 경우	- 두 모집단의 분산 간    비율에 대해 검정 - F = s₁² / s₂²

 
 

• 적합도 검정 (Goodness of Fit Test): 표본집단의 분포가 주어진 특정 이론을 따르고 있는지 검정
  
  
• 적합도 검정 기법
  - 가정된 확률이 정해진 경우 ⇒ 카이제곱 검정
  - 가정된 확률이 없는 경우 ⇒ 정규성검정: 샤피로-윌크 검정/ 콜모고로프-스미르노프 검정/ Q-Q Plot

 

샤피로-윌크 검정 Shapiro-Wilk Test	콜모고로프-스미르노프 검정 K-S Test	Q-Q Plot
- H0: 표본은 정규분포를 따른다 - 데이터 개수가 적은 경우	- 데이터가 어떤 특정한 분포를 따르는가 - 비교기준을 정규분포 데이터로 둔다 - 데이터 개수가 많은 경우	- 그래프: 시각적으로 검정 & 보조용 - 대각선 참조선을 따라서 데이터값들이   분포하면, 정규성 분포를 만족한다고 판단
R: shapiro.test()	R: ks.test()	기준 모호 & 결과해석 주관적

 

---

 

• 과대 적합 & 일반화

 

과대 적합 Over-fitting	일반화 Generalization
제한된 학습 데이터셋에 지나치게 특화되어, 새로운 데이터에 대한 오차가 매우 커지는 현상	- 테스트 데이터에 대해 높은 성능을 갖춤 - 정상 추정 O
- 모델 파라미터 개수가 많은 경우 - 학습 데이터 개수가 부족한 경우	- 과소 적합 X - 과대 적합 X

 
 

• 과대 적합 방지: 데이터 증강/ 모델복잡도 감소/ 가중치 규제/ 드롭아웃

 

데이터 증강	모델의 복잡도 감소	가중치 규제 적용	드롭아웃 Dropout
- 학습데이터 양이 적은 경우 - 데이터를 변형하여 늘림	- 인공신경망의 복잡도 감소 - 은닉층의 개수 감소↓ - 모델의 수용력 낮춤↓	- 개별 가중치 값을 제한하여   복잡한 모델을 간단하게 함 - L1규제 & L2규제	- 학습과정에서 신경망   일부를 사용하지 않음 - 예측과정에서는 사용 X

 
 

• 가중치 규제 적용

 

가중치 규제 개념		가중치 규제 종류
비용함수	하이퍼파라미터 λ	L1 규제 λ |w|	L2 규제 (1/2) λw²
- 관측값-연산값 차이 도출 - 비용함수 최소화를 위해   가중치들 값이 작아져야 함	- 규제 강도를 정함 - λ값 크면, 가중치 규제를   위해 추가한 항들을 작게 유지	모든 가중치들의 절댓값 합을 비용함수에 추가함	모든 가중치들의 제곱합을 비용함수에 추가함

 
 

• 드롭아웃 (Dropout): 학습과정에서 신경망 일부를 사용하지 않는 과대적합 방지 방법

 

드롭아웃 특징	초기 드롭아웃 DNN	공간적 드롭아웃 CNN	시간적 드롭아웃 RNN
- 특정 뉴런/조합에 너무 의존    적인 신경망이 되는 것 방지 - 매번 랜덤으로 뉴런 선택 - 앙상블과 같은 효과 - 학습과정 O 예측과정 X	- p의 확률로 노드들을 생략 (ex) 일반적으로 p = 0.5          학습과정마다 랜덤으로          절반의 뉴런을 사용X - DNN 심층신경망에서 사용	- 특징맵 내의 노드 전체에   대해 드롭아웃 적용여부 결정 - CNN 합성곱신경망에서 사용	- 노드가 아니라,    연결선 일부를 생략하는 방식 - RNN 순환신경망에서 사용

 
 

• 매개변수/ 매개변수 최적화

 

매개변수 Parameter	매개변수 최적화 Parameter Optimization
주어진 데이터로부터 학습을 통해, 모델 내부에서 결정되는 변수	- 손실함수: 학습모델의 출력값과 실제값의 차이 (오차) - 모델의 학습 목적: 오차/손실함수 값을 최대한 작게 하도록 하는    매개변수(가중치, 편향)을 찾는 것 ⇒ 매개변수 최적화
- 가중치 (Weight): 입력값마다 각기 다르게 곱해지는 수치 - 편향 (Bias): 가중합에 더해주는 상수	- 2차원 손실함수 그래프(X축:가중치, Y축:손실값)를 이용함 - 손실값 최소화 지점 = 그래프에서 기울기가 0인 지점 - 학습률이 적당해야 찾을 수 있음!

 
 

• 매개변수 최적화 기법: 확률적 경사 하강법 →<단점 개선>→ 모멘텀/ AdaGrad/ Adam
• SGD의 단점: 손실함수 그래프에서 지역극소점(Local)에 갇혀, 전역극소점(Global)을 찾지 못하는 경우가 발생함

 

확률적 경사 하강법 SGD	모멘텀 Momentum	AdaGrad	Adam
- 손실함수 기울기를 따라   조금씩 아래로 내려감 - 손실함수 최소지점에 도달 - 학습 1회에 필요한 데이터를   무작위로 선택함 (확률적)	- 모멘텀 = SGD + 속도 - 누적된 기울기 값에 의해   빠르게 최적점으로 수렴 - 관성의 방향을 고려하여   진동&폭을 줄이는 효과	- 진행할수록 학습률 감소↓ - 손실함수 처음 부분에선,   기울기&학습률이 크다 - 최적적에 가까워지면,   기울기&학습률이 크게 감소	- Adam = 모멘텀 + AdaGrad - 탐색경로 또한 모멘텀과    AdaGrad를 합친 양상
- 최적점 근처에서 느림 - 지그재그로 크게 변함	- SGD보다 지그재그 덜함 - 공이 그릇바닥을 구르듯!	- 지그재그 움직임이   크게 줄어든다 (효율적 움직임)	- 모멘텀보다 좌우흔들림↓ - 공이 그릇바닥을 구르듯~

 
 

• 분석 모형 융합 - 취합(Aggregation) & 부스팅(Boosting)

 

취합 방법론		부스팅 방법론
다수결	여러모형의 결과를 종합 직접투표/ 간접투표(가중치)	하나의 모형에서 시작하여, 각 약한 모형을 순차적으로 추가
배깅	복원추출로 학습데이터 나눔 중복 허용 → 편향 가능성O	에이다 부스트	- 정분류 샘플: 가중치 낮춤↓ - 오분류 샘플: 가중치 높임↑
페이스팅	비복원추출 → 중복 허용 X	그래디언트 부스트	오분류 샘플의 에러를 최적화
랜덤 서브스페이스	특성 샘플링
랜덤 패치	특성&학습데이터 둘다 샘플링
랜덤 포레스트	독립변수 차원을 랜덤하게 감소시킨 다음, 그중에서 선택

 
 

• 최종 모형 선정: 최종모형 평가기준 선정 → 최종모형 분석결과 검토 → 알고리즘별로 결과 비교

 
 

---

 
참고 도서: 빅데이터분석기사 필기_수제비 2021